At school, children learn not only to read, write, count in the mind, but also to multiply, to share large numbers without a calculator. Such skills are always useful. Thanks to such knowledge, it will be difficult for you in the store and not only, knowledge will be useful in practice. It is difficult for many to be divided into a column at school, if you can’t do this in the lessons, then study the material below.
Contents
Division into a column is difficult for children, because for this you need to know what a divisor is, divided, private, and a multiplication table. It is also required to be able to divide the numbers into dozens, units, hundreds, etc. Also, in the process of division, you have to subtract and add numbers, preferably in the mind. To begin with, of course, you can use drafts, but when it comes to automatism, you can’t make it difficult to divide the five -digit numbers into a column into two -digit, three -digit and four -digit.
Division into a column of two -digit, three -digit, multi -digit numbers, numbers with zeros
You do not need to be scared immediately that the division process is not simple, so you will not master it. Make up! In mathematics, clear rules should be observed, then you will succeed. The division algorithm is better to teach by specific examples, many examples will be presented below.
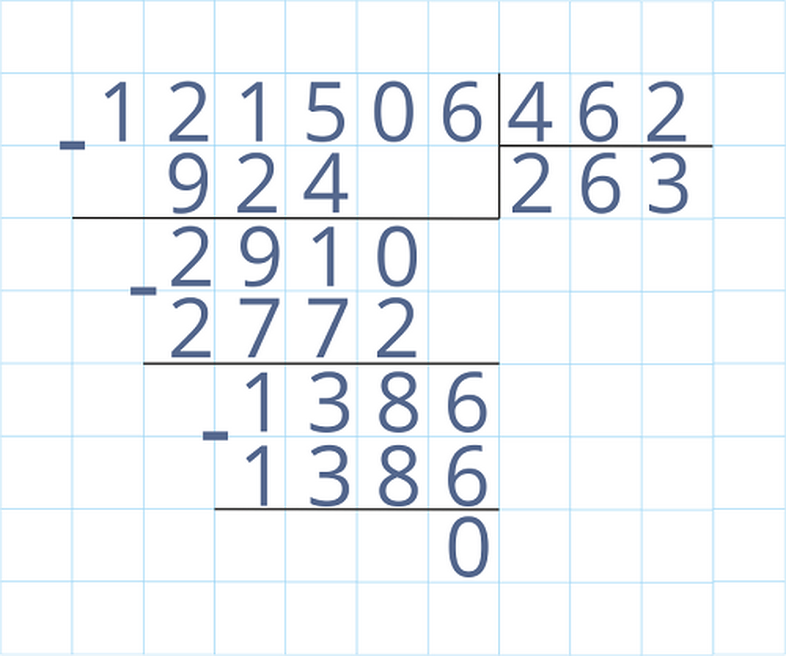
All of them are performed according to the scheme:
- First, divisible is recorded, a badge is placed nearby divide: ι -, and above the line the divider is written (the number that is divided into divisible).
- Then it is necessary to distinguish part of the divisible to carry out division, if necessary in this case.
- Next, you will have to multiply in order to determine how many times to take the divider in order to get the allocated part of the divided. Moreover, the number should not be more than 9.
- Perform multiplication of the dividerWrite down result Under divisible, and number ≤ 9 Write under the line of the sign: Ι - divide.
- Subtract from the selected part of the divisible result,write it down under emphasis, demolish the following the figure is divided,repeat the multiplication process again until you divide the number by the number.
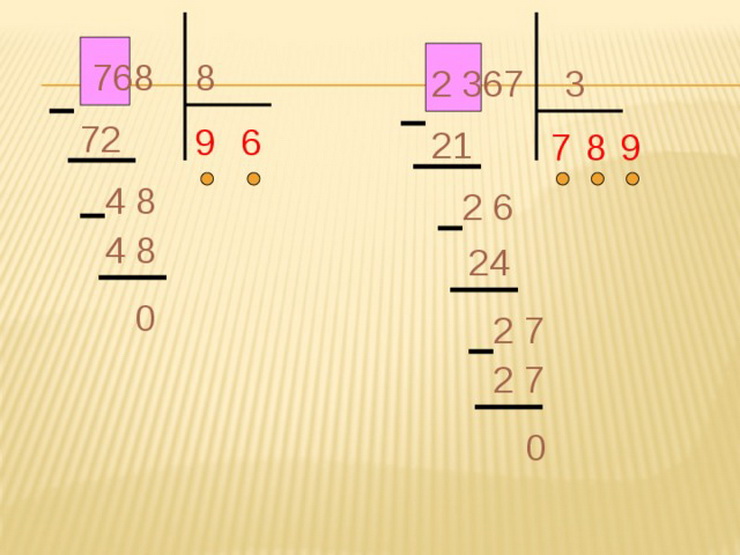
Consider the division into a column on a simple example:
If such two -digit numbersAs 16, 28 can be divided into the mind by 2 or 4 (in the first case, when dividing by 2 it turns out 8 and 14), and in the second (4 and 7), then 51 divided into 3 without a column is already more difficult. How the division in the column will be signed on example 51 divide into 3.

- As divisible is recorded, the divider has already been said, visually you can see higher in the image. Diviming is the first, then the division icon is placed and the divider is written above the line.
- Now we decide how much the numbers are highlighted in order to start selecting a multiplier that is recorded under the line in the highlighted square in the image.
- We highlight one digit of 5-ku, it is more than 3, on the draft, write about which one to choose what the multiplier is to get the number ≤ 5, it looks like this: 5 ≥ 3 · 1, the number 1 is a multiplier. It is written under the line to divide in a square.
- Next, under the five, we write a product 3 · 1 \u003d 3.
- Now we subtract from 5 - 3 \u003d 2. The difference, in our case 2 there should be a divider, in our case 3.
- So, it remains to divide 21 by 3. From the multiplication table you know that: 21: 3 \u003d 7.
- The seven is written under the line of the icon to divide after one. The answer is 17.
IMPORTANT: Remember - no numbers can be divided into 0 at all.
Next, we consider an example of the division of three -digit numbers:
Let's divide three -digit number 512 by 16. The division will occur according to the same scheme as a two -digit number.

- Write down divisible, divisor, as in the photo above.
- Next, we select the number 51, and find out how many times you need to take the number 16 so that the work is less or equal to 51. So, the calculations are presented above: 16 · 3 \u003d 48 ‹51.
- So write 3 under the line, and under the divisible 48. Now from 51, read 48, get 3, demolish the next number 2.
- Choose the multiplier to 16 so that the work turns out equal or less than 32. Total: 16 · 2 \u003d 32.
- Write down the deuce under the line of the sign of division, and the result is 32 under the divided. Total 32 - 32 \u003d 0.
- Result 32.
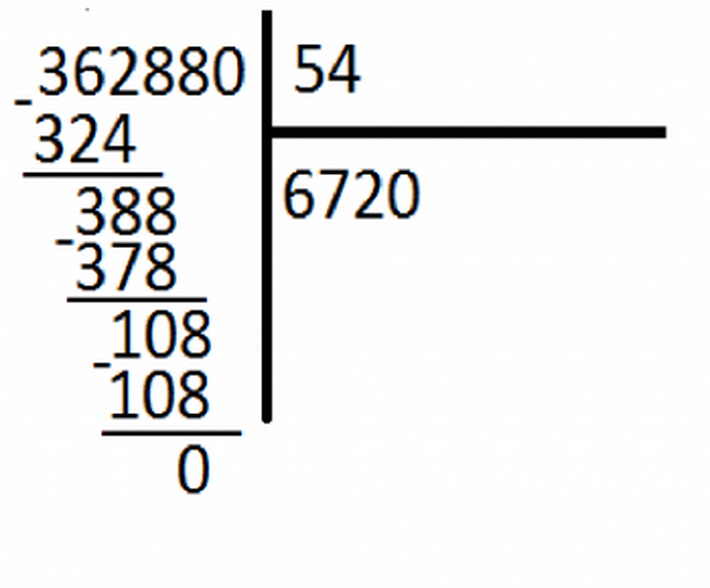
Consider the division of a multi -valued number:
Let's find private 998190 on 135, the example is presented in the image below. To solve it, you should set the necessary numbers in empty cells.

- So you need to find the first digit, for which you need to multiply the number 135 to get the result ≤ 998. For this you will need to know the multiplication table and the ability to fold numbers perfectly. 135 · 7 = 945.
- Write the number 945 under divisible, read from 998 - 945 \u003d 53. This number is less than 135, therefore you need to demolish another number 1, it will turn out 531.
- We calculate which factor is suitable, to 135 to get a number less than 534. Decision: 135 · 3 \u003d 405.
- The second digit Under the line of the sign of division 3,from 531 - 405 \u003d 126.
- Demolish 9, it comes out 1269, select the multiplier to 135. The result is 135 · 9 \u003d 1215.
- The third digit Under the line 9.Now: 1269 - 1215 \u003d 54.
- Demolish 0, it comes out 540, and 540 \u003d 135 · 4, total the last figure of the result is 4.
- The result is 7394.
Division of numbers with zeros:
Please note that if zeros are present at the end of the divided and divider, then it is better to cross out with a pencil or as they say, to reduce the divisible, and the divider by 10 or 100, and maybe 1000 units. For example, 512000: 16000, and the divisor and divided by divisible by 1000, it will turn out 512: 16, while the result will be true that with zero, what without them \u003d 32. When 0 is available only in the divider, then it should also be reduced and divided and divided and divided. The divider (in our case by 10), then divide, as usual, given the commas in numbers, example: 634.5: 9 \u003d 70.5.
Division into a column - rules
In order to be able to divide in a column, you need to know some rules. This is what will be further about. After all, the division into a column cannot be mastered if you do not know the elementary - multiplication tables. Counting simple examples of multiplication must be quickly and in the mind. It is only at the beginning that children usually use drafts to choose a multiplier, thus find a private one. It is also necessary to be able to break the numbers by hundreds, dozens, thousands - not to get confused in these concepts. For clarity, where is divided, where the divisor, where the private can study the terms in the image below.
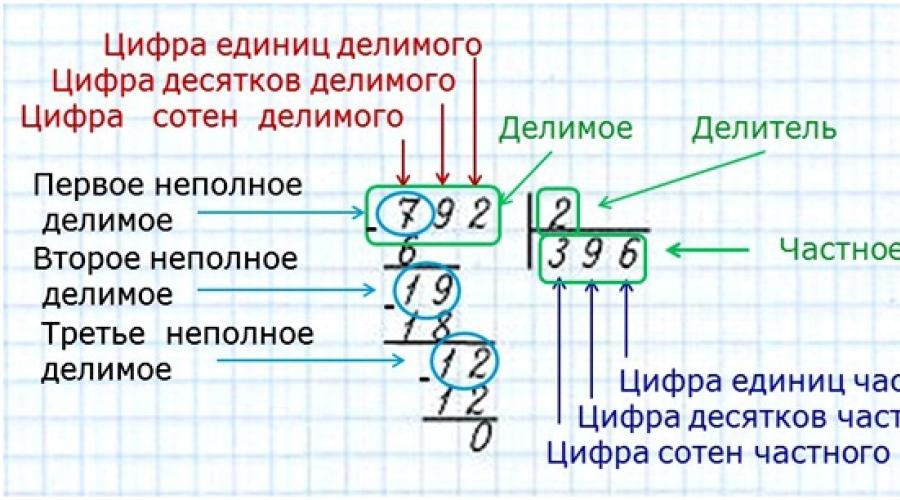
Before proceeding with division, you should check the child for knowledge of elementary rules. After all, it is impossible to miss mathematics. And if there were still gaps, then you need to study the material that was previously studied at school lessons. You will need to pay attention to such knowledge as:
- Whether the schoolboy remembered, what are all elements involved in the division process.
- Pay attention to the knowledge of the multiplication table by the child.
- Another child should learn what catrains of the number (units, dozens, hundreds).
It is necessary to form a clear understanding of division into a column as a process in mathematics. If the student did not understand the essence, then the task of adults to help him with this problem. Understand what dividend is a number that is divided into equal shares, and divider - the number indicates how much the previous number of parts is needed to get the result is private.
Example:
- 57: 3, where 57 is divided, the number that is divided into shares, and 3 - this is the dividerindicating how much to divide the previous number.
- We determine, first, which units to be distinguished in divisible for the implementation of division in a column of number 57. Number 5 ›3.
- Find out how many times should you take the number 3 to get 5. The result 3 · 1 \u003d 3 ≤ 5.So it comes up 1 Put as the first number private.
- Now subtracting: 5 - 3 \u003d 2.The remainder is 2 and we demolish the unit, it comes out 27.
- We find now how much you need to multiply 3so that the result is 27.According to the multiplication table 3 · 9 \u003d 27.
- Total result 19.
Multiplication, division - interconnected, albeit opposite operations. To check whether the private is found correctly, it is necessary to multiply. Therefore, the multiplication table and the ability to multiply on a draft without a calculator will always be useful to the child, also when multiplying, you should be able to add correctly, and deducted in the column when dividing. In mathematics, all actions with numbers are interconnected.
Below, see an example of division into a column 536 by 4. Actions with a three -digit divisible are performed similarly as with a two -digit one.

The division at school begins to be taught from the third grade.Schoolchildren only study the basics of the process, perform the simplest examples on this action.
Examples are similar to multiplication, only children are taught a division table, not multiplication. Schoolchildren should catch the very essence, which means dividing the number into several parts, studying what is divided, divisor, private. They learn how to check with multiplication the correctness of a solution to an example or a problem. Children do not yet consider the column, since the simplest examples are given and all numbers from the multiplication table. Example: 81 : 9 = 9.
The division process in the fourth grade is significantly complicated.At the beginning of the year, children are given to remember what they taught in the third grade, and then they begin to master the technique of dividing numbers into a column. It is during this academic year that such knowledge is mastered. Below is an algorithm for solutions to a column with a detailed description of the process.

Here it is even taken into account that it will be possible to be the remainder during the division, that the number will turn out not whole, but through a comma.
Division into a column - examples for training
Without many examples, it is difficult to master the technique of dividing into a column. You can cut a bunch of examples and then in any case the material will learn well. Below is an example of dividing the number 748 by 2. Let's analyze this simple example of division into a column.
- The divisible should be distinguished hundreds, more precisely, 7 of them are divided. For this number we select the factor: 2 · 3 \u003d 6 ≤ 7So it is suitable.
- We write 6 under the seven, and 3 under the line, this is one of private numbers.
- We subtract from 7 - 6 \u003d 1, and demolish 4. Now we select the multiplier: 2 · 7 \u003d 14 \u003d 14 - the result is correct. The second digit is private 7.
- We write 14 under 14, and demolish the next figure of the divided eight.We select the multiplier: 2 · 4 \u003d 8 \u003d 8,the difference is 0, the number is divided without a trace.
- So, the result 374.
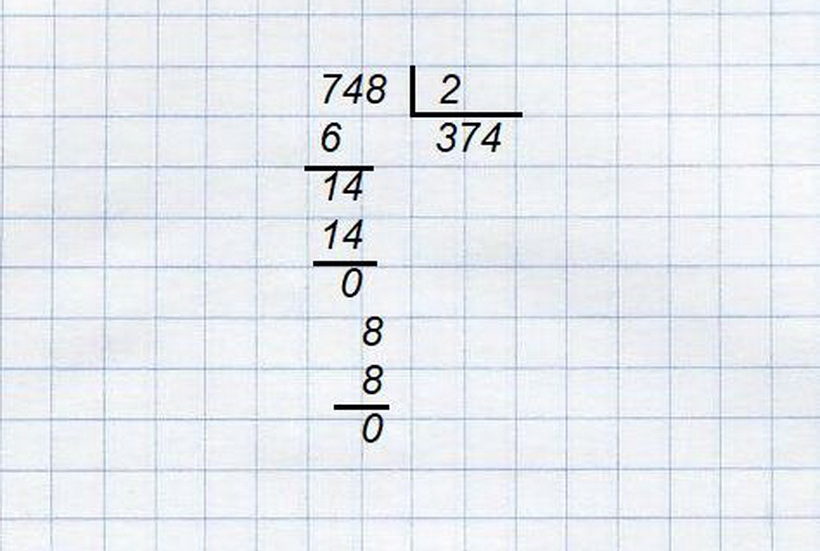
This example is resolved, there are many other examples that will be presented further in the text in the photo. These examples are a ready -made solution to home tasks, where the process of dividing into a column is described in detail, as each number of private is located. When you cut all of them yourself, the case will come to automatism and you can solve the task of any complexity using your skill.
To divide into a column, perhaps, one of the most difficult topics in mathematics. As already mentioned, all four actions are used in the process (starting from addition, ending with multiplication). You can’t do without knowledge of these processes. Some people think that why is to know, how to share if there are calculators. But they are not always at hand, but it is necessary to calculate the change or another value, and knowledge will be useful in practice. Next, study examples on this topic.
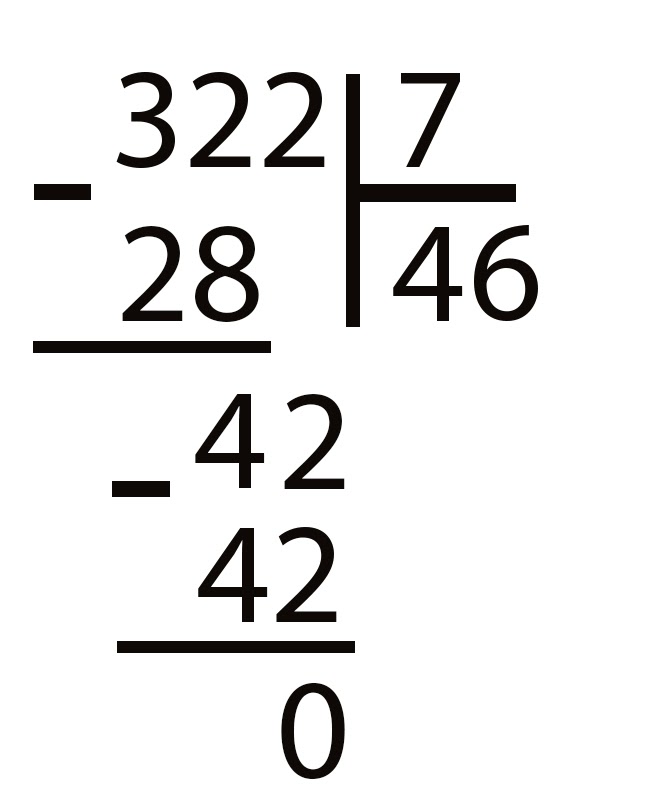



Here, on the portal, you can learn a lot of interesting things on the topic of education in these texts:
- The fairy tale "Turnip" by roles in school;
- Essay on Krylov’s fable “Crow and Fox”;
- Essay on the topic "My future profession";
- Counters for children of different ages;
- How to write correctly - to health?







