ที่โรงเรียนเด็ก ๆ เรียนรู้ไม่เพียง แต่อ่านเขียนนับในใจ แต่ยังทวีคูณเพื่อแบ่งปันจำนวนมากโดยไม่ต้องเครื่องคิดเลข ทักษะดังกล่าวมีประโยชน์เสมอ ด้วยความรู้ดังกล่าวมันจะเป็นเรื่องยากสำหรับคุณในร้านค้าและไม่เพียง แต่ความรู้จะเป็นประโยชน์ในการปฏิบัติ เป็นเรื่องยากสำหรับหลาย ๆ คนที่จะแบ่งออกเป็นคอลัมน์ที่โรงเรียนหากคุณไม่สามารถทำสิ่งนี้ได้ในบทเรียนจากนั้นศึกษาเนื้อหาด้านล่าง
สารบัญ
การแบ่งออกเป็นคอลัมน์เป็นเรื่องยากสำหรับเด็กเพราะสิ่งนี้คุณต้องรู้ว่าตัวหารคืออะไรแบ่งแยกส่วนตัวและตารางการคูณ นอกจากนี้ยังต้องสามารถแบ่งตัวเลขออกเป็นหลายสิบหน่วยหลายร้อย ฯลฯ นอกจากนี้ในกระบวนการแบ่งคุณต้องลบและเพิ่มตัวเลขโดยเฉพาะอย่างยิ่งในใจ ในการเริ่มต้นแน่นอนคุณสามารถใช้ร่างได้ แต่เมื่อพูดถึงระบบอัตโนมัติคุณไม่สามารถแบ่งตัวเลขห้าตัวออกเป็นคอลัมน์ออกเป็นสองตัวสามตัวสามตัวและสี่ตัว
แบ่งออกเป็นคอลัมน์ของสอง -digit, สาม -digit, ตัวเลขหลายตัว, ตัวเลขที่มีศูนย์
คุณไม่จำเป็นต้องกลัวทันทีว่ากระบวนการแบ่งไม่ง่ายดังนั้นคุณจะไม่เชี่ยวชาญ แต่งหน้า! ในวิชาคณิตศาสตร์ควรปฏิบัติตามกฎที่ชัดเจนแล้วคุณจะประสบความสำเร็จ อัลกอริทึมการแบ่งจะดีกว่าที่จะสอนโดยตัวอย่างเฉพาะตัวอย่างจำนวนมากจะถูกนำเสนอด้านล่าง
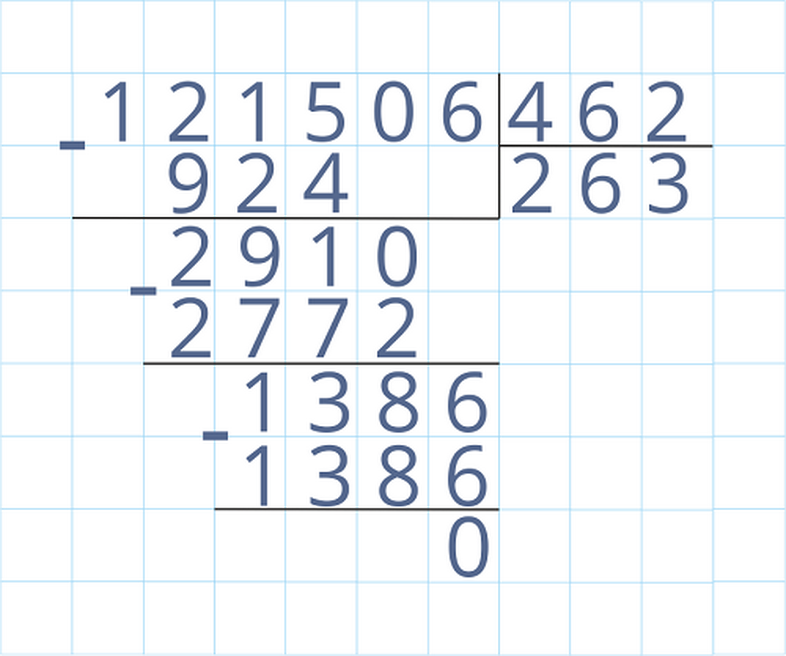
พวกเขาทั้งหมดดำเนินการตามโครงการ:
- ก่อนอื่น Divisible จะถูกบันทึกไว้ตราวางอยู่ใกล้ ๆ หาร: ι -และเหนือบรรทัดตัวแบ่งจะถูกเขียน (จำนวนที่แบ่งออกเป็นหาร)
- จากนั้นจำเป็นต้องแยกแยะส่วนหนึ่งของการแบ่งแยกเพื่อดำเนินการแบ่งหากจำเป็นในกรณีนี้
- ถัดไปคุณจะต้องทวีคูณเพื่อกำหนดจำนวนครั้งที่จะใช้ตัวแบ่งเพื่อให้ได้ส่วนที่จัดสรรของการแบ่งแยก ยิ่งกว่านั้นจำนวนไม่ควรเกิน 9
- ดำเนินการ การคูณของตัวแบ่งเขียนลงไป ผลลัพธ์ ภายใต้การแบ่งแยกและ จำนวน≤ 9 เขียนภายใต้บรรทัดของเครื่องหมาย: ι - หาร.
- ลบออกจากส่วนที่เลือกของหารได้ ผลลัพธ์,เขียนมันลงไปภายใต้การเน้นทำลายสิ่งต่อไปนี้ รูปแบ่งออกทำซ้ำกระบวนการคูณอีกครั้งจนกว่าคุณจะหารหมายเลขด้วยหมายเลข
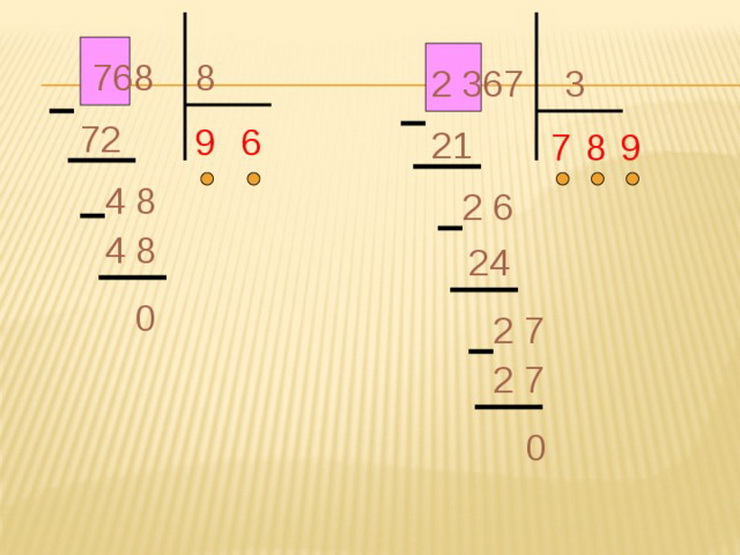
พิจารณาการแบ่งเป็นคอลัมน์ในตัวอย่างง่ายๆ:
ถ้าเช่นนั้น ตัวเลขสองตัวเป็น 16, 28 สามารถแบ่งออกเป็น 2 หรือ 4 (ในกรณีแรกเมื่อหารด้วย 2 ปรากฎ 8 และ 14) และในวินาที (4 และ 7) จากนั้น 51 แบ่งออกเป็น 3 โดยไม่มีคอลัมน์ ยากขึ้นแล้ว การแบ่งในคอลัมน์จะลงนามในตัวอย่าง 51 แบ่งออกเป็น 3

- เมื่อบันทึกการหารถูกบันทึกตัวหารได้รับการกล่าวไปแล้วว่าคุณสามารถมองเห็นภาพที่สูงขึ้นได้ Diviming เป็นครั้งแรกจากนั้นจึงวางไอคอนส่วนและตัวแบ่งจะถูกเขียนขึ้นเหนือบรรทัด
- ตอนนี้เราตัดสินใจว่าตัวเลขจะถูกเน้นเท่าใดเพื่อเริ่มเลือกตัวคูณที่บันทึกไว้ภายใต้บรรทัดในตารางไฮไลต์ในภาพ
- เราเน้นหนึ่งหลักของ 5-ku มันมีมากกว่า 3 ในร่างเขียนเกี่ยวกับสิ่งที่จะเลือกสิ่งที่ตัวคูณคือการได้รับหมายเลข≤ 5 ดูเหมือนว่า: 5 ≥ 3 · 1 หมายเลข 1 เป็นตัวคูณ มันเขียนไว้ใต้เส้นเพื่อแบ่งเป็นสี่เหลี่ยมจัตุรัส
- ถัดไปภายใต้ห้าเราเขียนผลิตภัณฑ์ 3 · 1 \u003d 3
- ตอนนี้เราลบออกจาก 5 - 3 \u003d 2 ความแตกต่างในกรณีของเรา 2 ควรมีตัวแบ่งในกรณีของเรา 3
- ดังนั้นจึงยังคงแบ่ง 21 โดย 3 จากตารางการคูณคุณรู้ว่า: 21: 3 \u003d 7
- ทั้งเจ็ดเขียนภายใต้บรรทัดของไอคอนเพื่อแบ่งหลังจากหนึ่ง คำตอบคือ 17.
สำคัญ: โปรดจำไว้ว่า - ไม่มีตัวเลขสามารถแบ่งออกเป็น 0 ได้เลย
ต่อไปเราจะพิจารณาตัวอย่างของการแบ่งหมายเลขสามตัวเลข:
มาแบ่งกัน หมายเลขสามมิติ 512 โดย 16. แผนกจะเกิดขึ้นตามรูปแบบเดียวกันกับหมายเลขสอง -ตัวเลข

- จดบันทึกหารตัวหารเช่นเดียวกับในภาพด้านบน
- ต่อไปเราเลือกหมายเลข 51 และค้นหาจำนวนครั้งที่คุณต้องใช้หมายเลข 16 เพื่อให้งานน้อยลงหรือเท่ากับ 51 ดังนั้นการคำนวณจะถูกนำเสนอด้านบน: 16 · 3 \u003d 48 ‹51
- ดังนั้นเขียน 3 ใต้บรรทัดและภายใต้ 48 ที่หารได้ตอนนี้จาก 51, อ่าน 48, รับ 3, ทำลายหมายเลขถัดไป 2
- เลือกตัวคูณเป็น 16 เพื่อให้งานเปลี่ยนไปเท่ากันหรือน้อยกว่า 32 ทั้งหมด: 16 · 2 \u003d 32
- เขียน deuce ใต้เส้นของสัญลักษณ์ของการแบ่งและผลลัพธ์คือ 32 ภายใต้การแบ่งแยก รวม 32 - 32 \u003d 0
- ผลลัพธ์ 32.
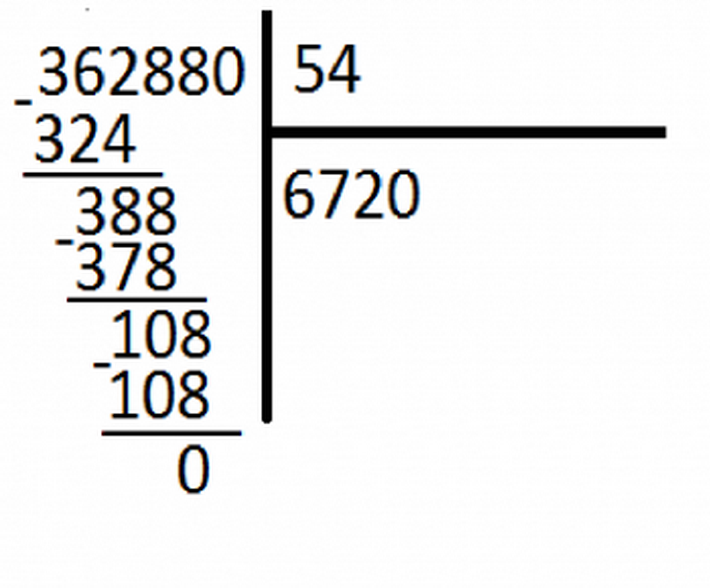
พิจารณาการแบ่งหมายเลขหลายค่า:
มาหา ส่วนตัว 998190 ในวันที่ 135ตัวอย่างจะถูกนำเสนอในภาพด้านล่าง ในการแก้ปัญหาคุณควรตั้งค่าตัวเลขที่จำเป็นในเซลล์เปล่า

- ดังนั้นคุณต้องค้นหา ตัวเลขแรกซึ่งคุณต้องคูณหมายเลข 135 เพื่อให้ได้ผลลัพธ์≤ 998 สำหรับสิ่งนี้คุณจะต้องรู้ตารางการคูณและความสามารถในการพับตัวเลขอย่างสมบูรณ์แบบ 135 · 7 = 945.
- เขียนหมายเลข 945 ภายใต้การหารอ่านจาก 998 - 945 \u003d 53 หมายเลขนี้น้อยกว่า 135 ดังนั้นคุณต้องรื้อถอนหมายเลข 1 อีกครั้งมันจะกลายเป็น 531
- เราคำนวณปัจจัยที่เหมาะสมถึง 135 เพื่อให้ได้ตัวเลขน้อยกว่า 534 การตัดสินใจ: 135 · 3 \u003d 405
- หลักที่สอง ภายใต้บรรทัดของสัญลักษณ์ของการหาร 3,จาก 531 - 405 \u003d 126
- รื้อถอน 9 มันออกมา 1269 เลือกตัวคูณเป็น 135 ผลลัพธ์คือ 135 · 9 \u003d 1215
- หลักที่สาม ใต้เส้น 9.ตอนนี้: 1269 - 1215 \u003d 54
- รื้อถอน 0 มันออกมา 540 และ 540 \u003d 135 · 4 ทั้งหมด รูปสุดท้ายของผลลัพธ์คือ 4.
- ผลลัพธ์คือ 7394.
ส่วนของตัวเลขที่มีศูนย์:
โปรดทราบว่าหากศูนย์อยู่ในตอนท้ายของการแบ่งแยกและตัวแบ่งแล้วมันจะเป็นการดีกว่าที่จะข้ามด้วยดินสอหรือตามที่พวกเขาพูดเพื่อลดการแบ่งแยกและตัวแบ่ง 10 หรือ 100 และอาจ 1,000 หน่วย ตัวอย่างเช่น 512000: 16000 และตัวหารและหารด้วยการหารด้วย 1,000 มันจะเปิดออก 512: 16 ในขณะที่ผลลัพธ์จะเป็นจริงว่าด้วยศูนย์สิ่งที่ไม่มีพวกเขา \u003d 32 เมื่อ 0 พร้อมใช้งานเฉพาะในตัวหารเท่านั้น จากนั้นก็ควรลดและแบ่งและแบ่งและแบ่งตัวหาร (ในกรณีของเราโดย 10) จากนั้นแบ่งตามปกติตามเครื่องหมายจุลภาคเป็นตัวอย่าง: 634.5: 9 \u003d 70.5
แบ่งออกเป็นคอลัมน์ - กฎ
เพื่อให้สามารถแบ่งในคอลัมน์คุณต้องรู้กฎบางอย่าง นี่คือสิ่งที่จะเพิ่มเติมเกี่ยวกับ ท้ายที่สุดการแบ่งออกเป็นคอลัมน์ไม่สามารถเข้าใจได้หากคุณไม่ทราบตารางการคูณเบื้องต้น การนับตัวอย่างง่ายๆของการคูณจะต้องรวดเร็วและอยู่ในใจ มันเป็นเพียงจุดเริ่มต้นที่เด็กมักจะใช้ร่างเพื่อเลือกตัวคูณดังนั้นจึงหาคนส่วนตัว นอกจากนี้ยังจำเป็นต้องสามารถทำลายตัวเลขได้หลายร้อยคนหลายสิบหมื่นคน - ไม่ต้องสับสนในแนวคิดเหล่านี้ เพื่อความชัดเจนที่ซึ่งแบ่งออกเป็นที่ซึ่งตัวหารที่ซึ่งส่วนตัวสามารถศึกษาคำศัพท์ในภาพด้านล่าง
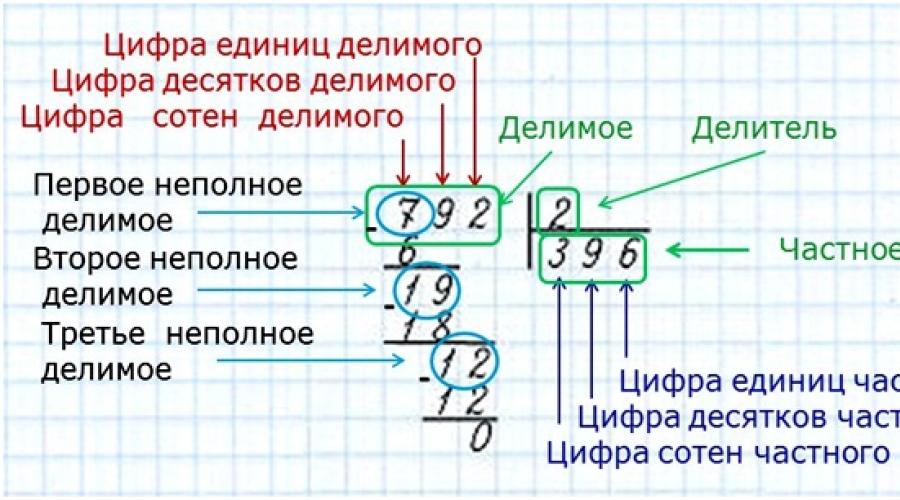
ก่อนดำเนินการกับการแบ่งคุณควรตรวจสอบเด็กเพื่อขอความรู้เกี่ยวกับกฎเบื้องต้น ท้ายที่สุดมันเป็นไปไม่ได้ที่จะพลาดคณิตศาสตร์ และถ้ายังมีช่องว่างคุณต้องศึกษาเนื้อหาที่เคยศึกษาก่อนหน้านี้ในบทเรียนของโรงเรียน คุณจะต้องให้ความสนใจกับความรู้เช่น:
- ไม่ว่าเด็กนักเรียนจะจำได้หรือไม่ องค์ประกอบทั้งหมดที่เกี่ยวข้องในกระบวนการหารคืออะไร
- ให้ความสนใจกับความรู้เกี่ยวกับตารางการคูณโดยเด็ก
- เด็กอีกคนควรเรียนรู้อะไร catrains ของจำนวน (หน่วย, หลายสิบ, หลายร้อย)
มีความจำเป็นที่จะต้องสร้างความเข้าใจที่ชัดเจนของการแบ่งเป็นคอลัมน์เป็นกระบวนการในวิชาคณิตศาสตร์ หากนักเรียนไม่เข้าใจสาระสำคัญงานของผู้ใหญ่ที่จะช่วยเขาแก้ปัญหานี้ เข้าใจอะไร เงินปันผล เป็นตัวเลขที่แบ่งออกเป็นหุ้นเท่ากันและ ผู้แบ่งแยก - ตัวเลขระบุจำนวนชิ้นส่วนก่อนหน้านี้เพื่อรับ ผลลัพธ์เป็นส่วนตัว
ตัวอย่าง:
- 57: 3, ที่ไหน 57 ถูกแบ่งออกจำนวนที่แบ่งออกเป็นหุ้นและ 3 - นี่คือตัวแบ่งระบุว่าจะหารหมายเลขก่อนหน้าเท่าไหร่
- เราพิจารณาก่อนอื่นหน่วยที่จะแตกต่างในการแบ่งแยกสำหรับการดำเนินการของการหารในคอลัมน์หมายเลข 57 5› 3.
- ค้นหาจำนวนครั้งที่คุณควรใช้หมายเลข 3 เพื่อรับ 5. ผลลัพธ์ 3 · 1 \u003d 3 ≤ 5ดังนั้นจึงเกิดขึ้น 1 ใส่เป็นหมายเลขแรก ส่วนตัว.
- ตอนนี้ลบ: 5 - 3 \u003d 2ส่วนที่เหลือคือ 2 และเราทำลายหน่วยมันออกมา 27.
- ตอนนี้เราพบว่าคุณต้องคูณมากแค่ไหน 3เพื่อให้ผลลัพธ์คือ 27.ตามตารางการคูณ 3 · 9 \u003d 27
- ทั้งหมด ผลลัพธ์ 19.
การคูณการหาร - เชื่อมต่อกันแม้ว่าการดำเนินการตรงข้าม เพื่อตรวจสอบว่าพบส่วนตัวอย่างถูกต้องหรือไม่จำเป็นต้องทวีคูณ ดังนั้นตารางการคูณและความสามารถในการทวีคูณในร่างที่ไม่มีเครื่องคิดเลขจะเป็นประโยชน์กับเด็กเสมอเมื่อการคูณคุณควรจะเพิ่มอย่างถูกต้องและหักในคอลัมน์เมื่อหาร ในวิชาคณิตศาสตร์การกระทำทั้งหมดที่มีตัวเลขเชื่อมต่อกัน
ด้านล่างดูตัวอย่างของการหารลงในคอลัมน์ 536 โดย 4 การกระทำที่มีสามมิติที่แบ่งออกได้จะดำเนินการในทำนองเดียวกันกับสอง -จุดหนึ่ง

แผนกที่โรงเรียนเริ่มได้รับการสอนจากชั้นประถมศึกษาปีที่สามเด็กนักเรียนศึกษาพื้นฐานของกระบวนการดำเนินการตัวอย่างที่ง่ายที่สุดในการกระทำนี้
ตัวอย่างมีความคล้ายคลึงกับการคูณเด็กเท่านั้นที่สอนตารางการแบ่งไม่ใช่การคูณ เด็กนักเรียนควรจับแก่นแท้ซึ่งหมายถึงการแบ่งจำนวนออกเป็นหลายส่วนศึกษาสิ่งที่แบ่งออกเป็นตัวหารส่วนตัว พวกเขาเรียนรู้วิธีการตรวจสอบด้วยการคูณความถูกต้องของการแก้ปัญหาตัวอย่างหรือปัญหา เด็ก ๆ ยังไม่ได้พิจารณาคอลัมน์เนื่องจากตัวอย่างที่ง่ายที่สุดจะได้รับและตัวเลขทั้งหมดจากตารางการคูณ ตัวอย่าง: 81 : 9 = 9.
กระบวนการแบ่งในเกรดสี่มีความซับซ้อนอย่างมีนัยสำคัญในช่วงต้นปีเด็ก ๆ จะได้รับการจดจำสิ่งที่พวกเขาสอนในชั้นประถมศึกษาปีที่สามจากนั้นพวกเขาก็เริ่มที่จะฝึกฝนเทคนิคการแบ่งตัวเลขออกเป็นคอลัมน์ มันเป็นช่วงปีการศึกษานี้ที่ความรู้ดังกล่าวมีความเชี่ยวชาญ ด้านล่างเป็นอัลกอริทึมสำหรับการแก้ปัญหาคอลัมน์ที่มีคำอธิบายโดยละเอียดของกระบวนการ

ที่นี่ยังคำนึงถึงว่ามันเป็นไปได้ที่จะเป็นส่วนที่เหลือในระหว่างการแบ่งจำนวนว่าจำนวนจะไม่ทั้งหมด แต่ผ่านเครื่องหมายจุลภาค
แบ่งออกเป็นคอลัมน์ - ตัวอย่างสำหรับการฝึกอบรม
หากไม่มีตัวอย่างมากมายมันเป็นเรื่องยากที่จะควบคุมเทคนิคการแบ่งออกเป็นคอลัมน์ คุณสามารถตัดตัวอย่างจำนวนมากจากนั้นในกรณีใด ๆ วัสดุจะเรียนรู้ได้ดี ด้านล่างเป็นตัวอย่างของการหารหมายเลข 748 ด้วย 2 ลองวิเคราะห์ตัวอย่างง่าย ๆ ของการแบ่งออกเป็นคอลัมน์
- การแบ่งแยกควรมีความโดดเด่นหลายร้อยอย่างแม่นยำยิ่งขึ้น 7 ของพวกเขาถูกแบ่งออก สำหรับหมายเลขนี้เราเลือกปัจจัย: 2 · 3 \u003d 6 ≤ 7ดังนั้นจึงเหมาะสม
- เราเขียน 6 ภายใต้เจ็ดและ 3 ภายใต้บรรทัดนี่เป็นหนึ่งใน หมายเลขส่วนตัว
- เราลบออกจาก 7 - 6 \u003d 1 และรื้อถอน 4. ตอนนี้เราเลือกตัวคูณ: 2 · 7 \u003d 14 \u003d 14 - ผลลัพธ์ถูกต้อง หลักที่สองเป็นส่วนตัว 7.
- เราเขียน 14 อายุต่ำกว่า 14 ปีและทำลายร่างต่อไปของการแบ่งแยก แปด.เราเลือกตัวคูณ: 2 · 4 \u003d 8 \u003d 8ความแตกต่างคือ 0 จำนวนจะถูกแบ่งโดยไม่มีการติดตาม
- ดังนั้นผลลัพธ์ 374.
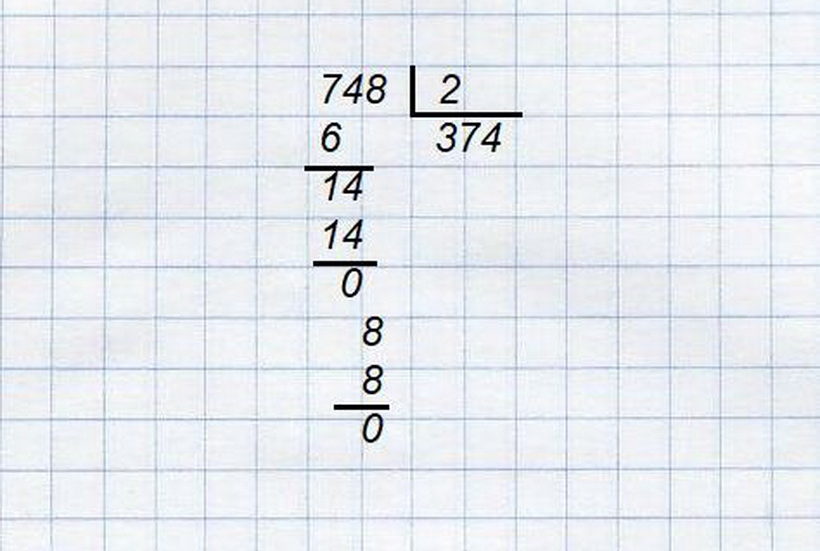
ตัวอย่างนี้ได้รับการแก้ไขมีตัวอย่างอื่น ๆ อีกมากมายที่จะนำเสนอเพิ่มเติมในข้อความในรูปภาพ ตัวอย่างเหล่านี้เป็นโซลูชันที่พร้อมใช้งานสำหรับงานบ้านซึ่งกระบวนการแบ่งออกเป็นคอลัมน์อธิบายรายละเอียดเนื่องจากแต่ละจำนวนส่วนตัวตั้งอยู่ เมื่อคุณตัดพวกเขาทั้งหมดด้วยตัวเองกรณีจะมาถึงระบบอัตโนมัติและคุณสามารถแก้ปัญหาความซับซ้อนใด ๆ โดยใช้ทักษะของคุณ
เพื่อแบ่งออกเป็นคอลัมน์บางทีหนึ่งในหัวข้อที่ยากที่สุดในคณิตศาสตร์ ดังที่ได้กล่าวไปแล้วการกระทำทั้งสี่นั้นใช้ในกระบวนการ (เริ่มต้นจากการเพิ่มโดยจบด้วยการคูณ) คุณไม่สามารถทำได้โดยปราศจากความรู้เกี่ยวกับกระบวนการเหล่านี้ บางคนคิดว่าทำไมต้องรู้วิธีการแบ่งปันหากมีเครื่องคิดเลข แต่พวกเขาไม่ได้อยู่ในมือเสมอไป แต่จำเป็นต้องคำนวณการเปลี่ยนแปลงหรือค่าอื่นและความรู้จะเป็นประโยชน์ในการปฏิบัติ ถัดไปศึกษาตัวอย่างในหัวข้อนี้
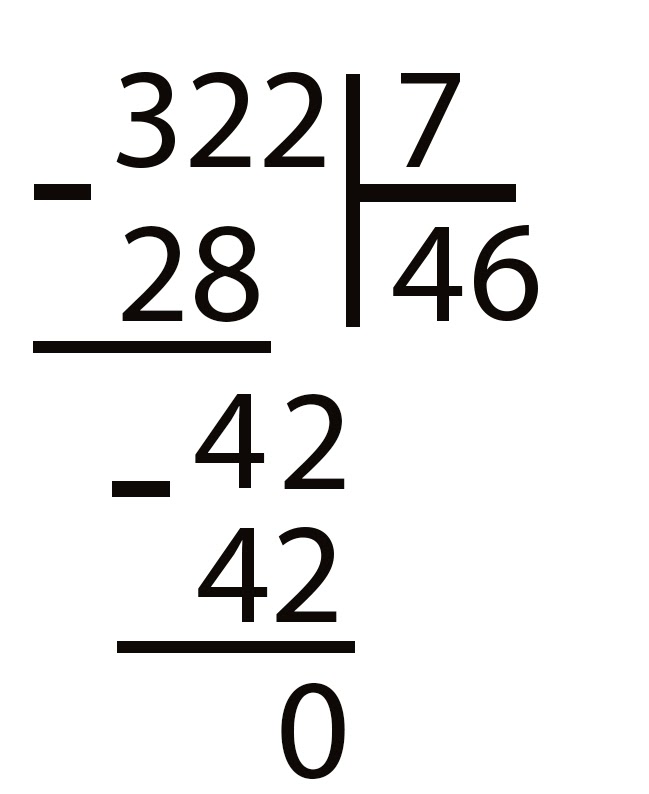



ที่นี่บนพอร์ทัลคุณสามารถเรียนรู้สิ่งที่น่าสนใจมากมายในหัวข้อการศึกษาในตำราเหล่านี้:
- เทพนิยาย "หัวผักกาด" โดยบทบาทในโรงเรียน;
- เรียงความเกี่ยวกับนิทานของ Krylov“ Crow and Fox”;
- เรียงความเกี่ยวกับหัวข้อ "My Future อาชีพ";
- เคาน์เตอร์สำหรับเด็กที่มีอายุต่างกัน
- วิธีการเขียนอย่างถูกต้อง - เพื่อสุขภาพ?







